library(vars)
data = readRDS("data/md.Rds")
y = cbind(p = data$CPI, y = data$NGDP, r = data$Repo7D)
var = VAR(as.ts(y), p = 4)
irf(var, impulse = "r", response = "p", ortho = TRUE) |> plot()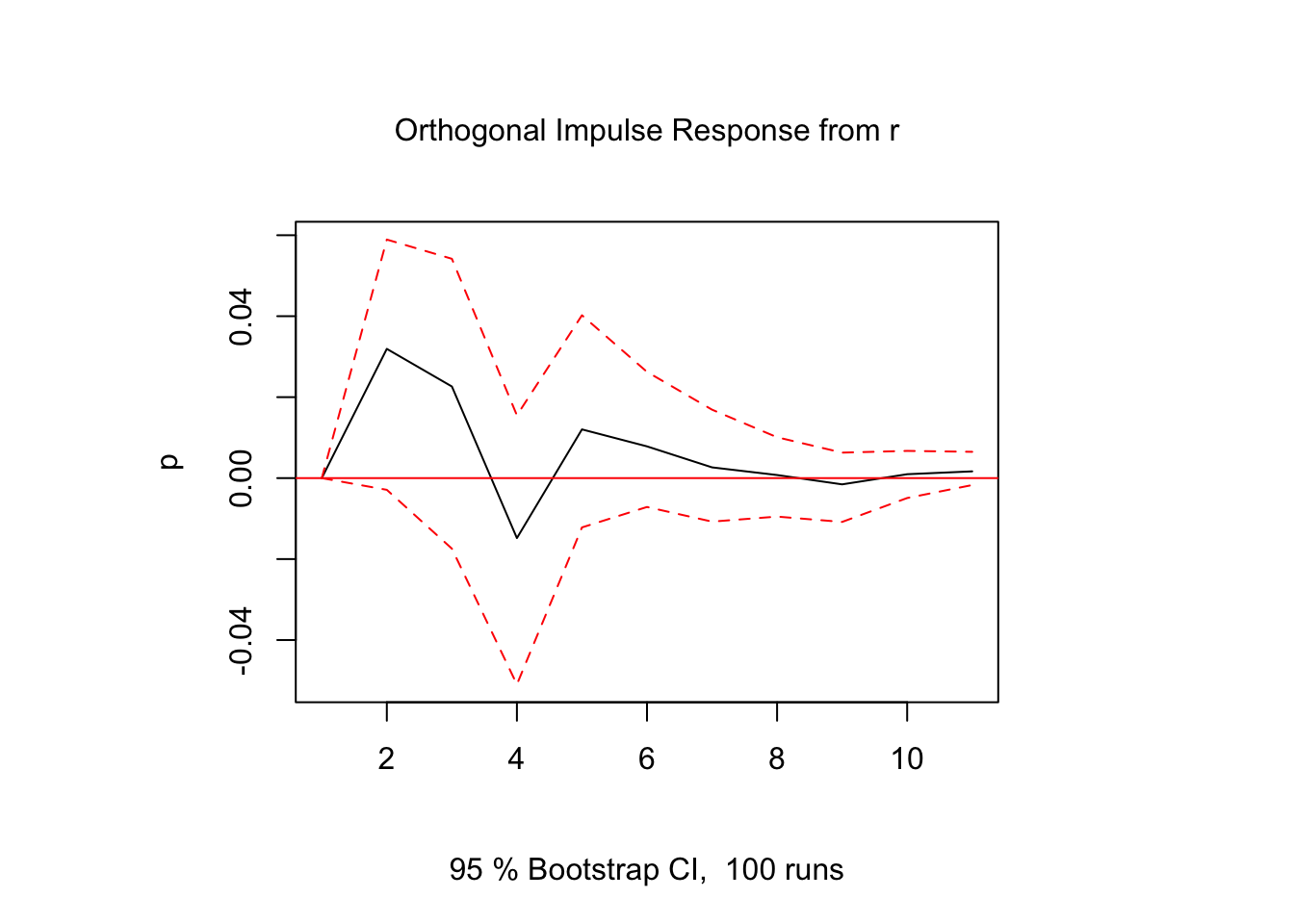
30 IRF and FEVD
30.1 Estimating SVAR
Given the Structural VAR,
\[ \Theta_0 y_t = \Phi_1 y_{t-1} + \Phi_2 y_{t-2} + \cdots + \Phi_p y_{t-p} + \epsilon_t \]
We estimate the reduced-form VAR using the methods in Chapter 27:
\[ y_t = A_1 y_{t-1} + A_2 y_{t-2} + \cdots + A_p y_{t-p} + u_t \]
where \(A_j = \Theta_0^{-1}\Phi_j\) and \(u_t = \Theta_0^{-1}\epsilon_t\). \(\Theta_0\) can be estimated using the identification scheme discussed in Chapter 29, so that the structural parameters can be recovered accordingly.
However, the coefficients of a VAR are difficult to interpret. For empirical analysis, we are particularly interested in estimating the impact of a structural shock on other economic variables (e.g. the impact of monetary policy shock on inflation). We cannot read off this information from the estimated VAR coefficients.
In this section, we introduce two reporting techniques: impulse-response functions (IRF) and forecast error variance decomposition (FEVD).
30.2 Impulse-Response Functions
With VAR parameters estimated, we can convert it to the MA form:
\[ y_t = A^{-1}(L)u_t = u_t + \Psi_1 u_{t-1} + \Psi_2 u_{t-2} + \cdots \]
or written in structural shocks:
\[ y_t = \Theta_0^{-1}\epsilon_t + \Psi_1\Theta_0^{-1}\epsilon_{t-1} + \Psi_2\Theta_0^{-1}\epsilon_{t-2} + \cdots \]
With this structural MA form, we can directly read off the impact of structural shock \(j\) on observable variable \(k\):
\[\frac{\partial y_{t+h}^k}{\partial\epsilon_t^j} = (\Psi_h\Theta_0^{-1})_{kj}\]
A sequence of the marginal impacts over time \(\left\{\frac{\partial y_{t}^k}{\partial\epsilon_t^j}, \frac{\partial y_{t+1}^k}{\partial\epsilon_t^j}, \frac{\partial y_{t+2}^k}{\partial\epsilon_t^j}, \dots\right\}\) constitute the dynamic response of variable \(k\) in response to structural shock \(j\), also known as the impulse-response function.
Note that \(\frac{\partial y_{t+h}^k}{\partial u_t^j}\) cannot be interpreted as the response of \(y_{t+h}^k\) after a shock on \(u_t^j\). Because \(u_t^j\) could be a linear combination of multiple structural shocks, e.g.
\[ u_t^1 =a_1\epsilon_t^1 + a_2 \epsilon_t^2 + a_3 \epsilon_t^3 \]
Therefore, no structural meaning can be attached to \(\frac{\partial y_{t+h}^k}{\partial u_t^j}\). But \(\frac{\partial y_{t+h}^k}{\partial\epsilon_t^j}\) is interpretable, as structural shocks \(\epsilon_t\) are uncorrelated.
If \(\Theta_0\) has a recursive structure, \(\Theta_0\) can be found simply by applying decomposition to the OLS-estimated \(\hat\Omega\):
\[ \hat\Omega=LDL' \]
If \(\hat\Omega\) is positive definite, such decomposition always exist, with \(D\) diagonal and \(L\) lower triangular with \(1\)s on the diagonal.
If we restrict \(D\) to be an identity matrix, the decomposition becomes
\[ \hat\Omega = PP' \]
where \(P = LD^{1/2}\). This is known as the Cholesky decomposition. By applying the Cholesky decomposition, we have
\[ \zeta_t = P^{-1}u_t = D^{-1/2}L^{-1}u_t = D^{-1/2}\epsilon_t \]
in which \(1\) unit shock to \(\zeta_t\) is equivalent to \(1\) standard deviation shock to \(\epsilon_t\). The IRFs estimated with Cholesky decomposition thus have the interpretation of response to standard-deviation shocks.
30.3 IRF Standard Errors
The IRF confidence intervals are usually constructed by bootstrapping.
- Estimate the VAR by OLS. Save residuals \(\hat u_1, \hat u_2, \dots, \hat u_T\).
- Randomly pick \(u_1\) from \(\{\hat u_1, \hat u_2, \dots, \hat u_T\}\), which will be used to construct an artificial sample. Generate \[y_1^{(1)} = \hat c + \hat\Phi_1 y_0 + \hat\Phi_2 y_{-1}+\cdots + \hat\Phi_p y_{1-p} + u_1^{(1)}\]where \(y_0, y_{-1},\dots y_{1-p}\) are pre-sampled values that were actually observed. Take a second draw \(u_2\). Generate \[y_2^{(1)} = \hat c + \hat\Phi_1 y_1 + \hat\Phi_2 y_{0}+\cdots + \hat\Phi_p y_{2-p} + u_2^{(1)}\]Proceed until \(\{ y_1^{(1)}, y_2^{(1)},\dots,y_T^{(1)} \}\) are generated. Run OLS on the simulated data, calculate the impulse-response function \(\{ \Psi_h^{(1)} \}\).
- Repeat the above step, generate \(\{ y_1^{(2)}, y_2^{(2)},\dots,y_T^{(2)} \}\). Estimate the IRF again \(\{ \Psi_h^{(2)} \}\). Repeat the process \(N\) times and get \(N\) IRFs. Sort them by \(\Psi^{(1)} \leq \Psi^{(2)} \cdots \leq \Psi^{(N)}\).
- The \(\alpha\) confidence interval is constructed as \([\Psi_{[N\alpha/2]}, \Psi_{[N(1-\alpha/2)]}]\).
30.4 FEVD
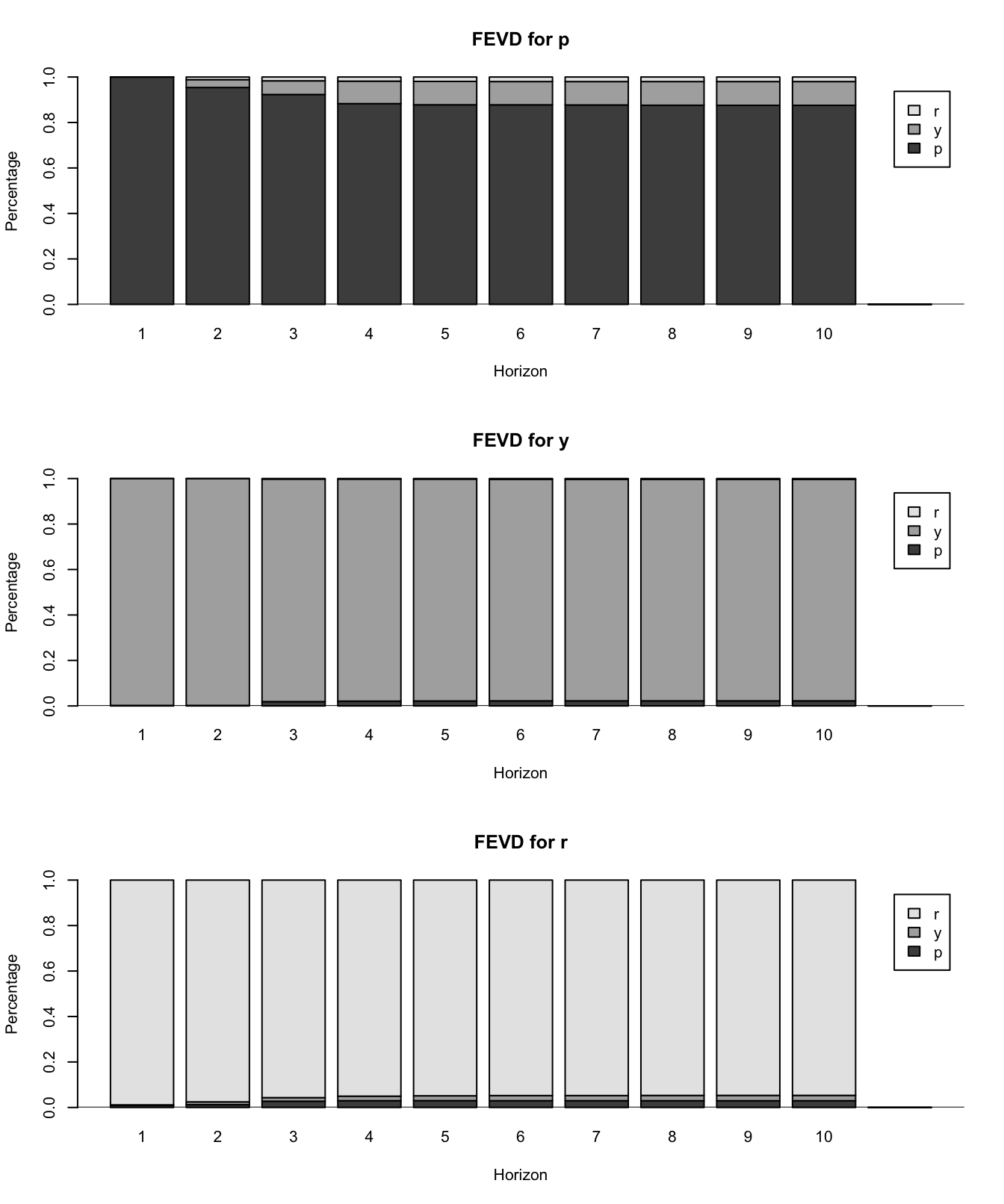
We would also like to know the relative importance of each structural force, which can be gauged by computing the forecast error variance decomposition (FEVD). Consider the forecast error
\[ y_{t+h} - \hat y_{t+h|t} = \Theta_0^{-1}\epsilon_{t+h} + \Psi_1\Theta_0^{-1}\epsilon_{t+h-1} + \cdots + \Psi_{h-1}\Theta_0^{-1}\epsilon_{t+1} \]
The mean squared error (MSE) is
\[ \begin{aligned} \text{MSE}(\hat y_{t+h|t}) &= \mathbb{E}[(y_{t+h} - \hat y_{t+h|t})(y_{t+h} - \hat y_{t+h|t})'] \\[1em] &= \Omega + \Psi_1\Omega\Psi_1' + \Psi_2\Omega\Psi_2' + \cdots + \Psi_{h-1}\Omega\Psi_{h-1}' \end{aligned} \]
where
\[ \begin{aligned} \Omega &= \mathbb{E}(\Theta_0^{-1}\epsilon_{t}\epsilon_{t}'{\Theta_0^{-1}}') \\ &= \begin{bmatrix} a_1 & a_2 & \dots & a_n \end{bmatrix} \begin{bmatrix} \text{var}(\epsilon_{1,t}) & & & \\ & \text{var}(\epsilon_{2,t}) & & \\ & & \ddots & \\ & & & \text{var}(\epsilon_{n,t}) \\ \end{bmatrix} \begin{bmatrix} a_1' \\ a_2' \\ \vdots \\ a_n' \end{bmatrix} \\[1em] &= a_1a_1'\text{var}(\epsilon_{1,t}) + a_2a_2'\text{var}(\epsilon_{2,t}) + \cdots + a_n a_n'\text{var}(\epsilon_{n,t}) \end{aligned} \]
Therefore,
\[ \text{MSE}(\hat y_{t+h|t}) =\sum_{j=1}^n \{ \text{var}(\epsilon_{j,t}) [a_ja_j' + \Psi_1a_ja_j'\Psi_1' + \cdots + \Psi_{h-1}a_ja_j'\Psi_{h-1}'] \} \]
The contribution of the \(j\)-th structural force to the MSE of the \(h\)-period-ahead forecast is given by
\[ \text{var}(\epsilon_{j,t}) [a_ja_j' + \Psi_1a_ja_j'\Psi_1' + \cdots + \Psi_{h-1}a_ja_j'\Psi_{h-1}']. \]
30.5 Example
fevd(var) |> plot()